机器人姿态简介

本文档主要介绍机器人姿态的多种表示方式，你将从本文档了解到以下内容：

1. 姿态有哪些常用的表示方法？
2. 这些表示方法有哪些特点和应用场景？
3. 这些表示方法怎么相互转换？

1. 姿态常用表示方式

1.1 旋转矩阵（Rotation Matrix）

采用一个 $3*3$ 的矩阵来表示旋转，即：

$R = \left[ \begin{matrix} \hat X & \hat Y & \hat Z \end{matrix} \right] = \left[ \begin{matrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{matrix} \right]$

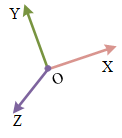
一个坐标系的三个坐标系轴的单位矢量确定一个姿态，我们用这三个单位矢量作为矩阵的列，即旋转矩阵来表示这个坐标系的姿态。

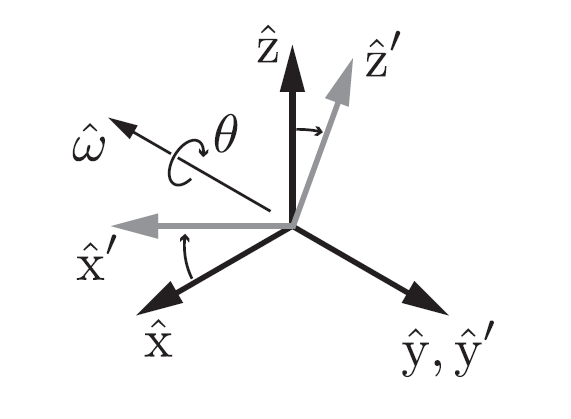
1.2 旋转矢量（Rotation Vector）

采用一个向量来表示旋转，即： $\vec v = \hat \omega \theta$

$R = Rot(\hat \omega, \theta)$ 其中： $\hat\omega = \left[ \matrix{\omega _1 \ \omega _2 \ \omega _3}\right]$ , 为旋转轴， $\theta$ 为绕 $\hat \omega $ 旋转的角度。

如下图所示：是一个绕 y 轴旋转 $\theta$ 角的一个示例

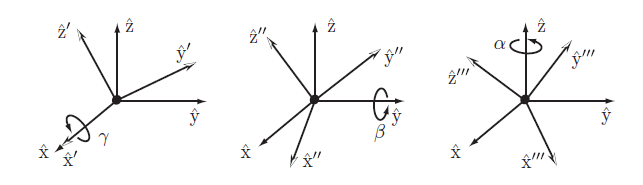
1.3 RPY角 (Roll-Pitch-Yaw Angles)

RPY 角采用三个角度绕固定坐标系转动的角度来表示旋转，

• 先绕固定坐标系的 $\hat X$ 轴旋转 $\gamma$ ；
• 再绕固定坐标系的 $\hat Y$ 轴旋转 $\beta$ ；
• 再绕固定坐标系的 $\hat Z$ 轴旋转 $\alpha$ ；

如下图所示：

可以表示为： $R(\alpha,\beta,\gamma) = Rot(\hat z,\alpha) Rot(\hat y,\beta) Rot(\hat x,\gamma)$

1.4 单位四元数（Unit Quaternions）

单位四元数采用四个数来表示一个旋转，已知一个旋转 $R = Rot(\hat \omega, \theta)$ ，采用四元数可以表示为 :

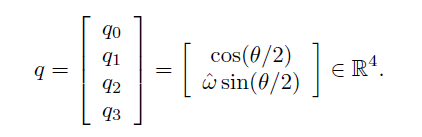
2. 相互转换

2.1 旋转矢量 和 旋转矩阵

• 旋转矢量转化到旋转矩阵

  

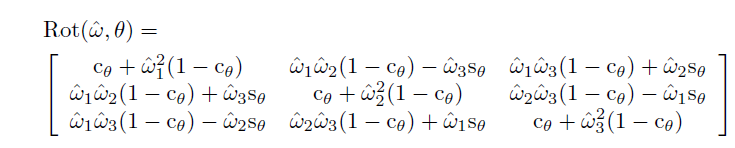
• 旋转矩阵转换到旋转矢量

  

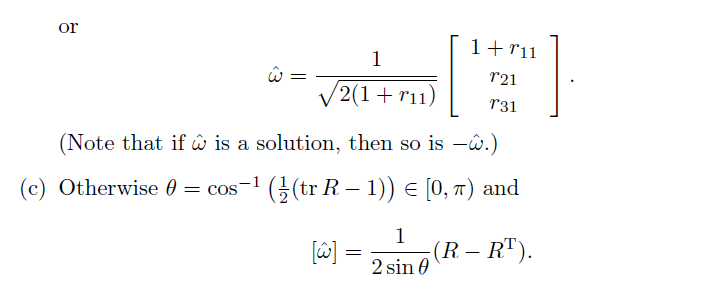
2.2 RPY 和 旋转矩阵

• RPY角转换为旋转矩阵

  

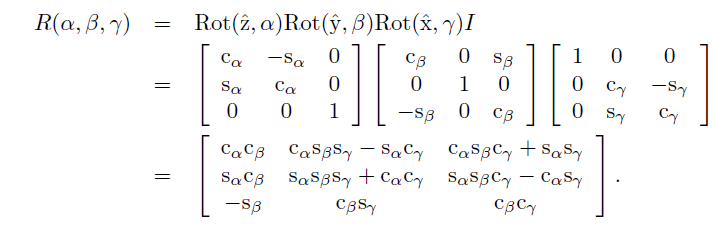
• 旋转矩阵转换为RPY角

  

2.3. 单位四元数 和 旋转矩阵

• 单位四元数转换到旋转矩阵

  

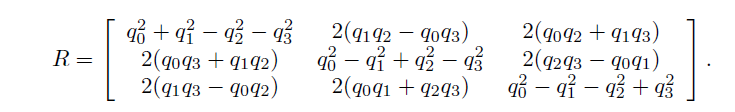
• 旋转矩阵转换到单位四元数

  

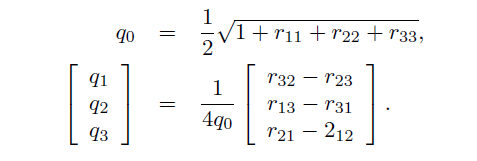
3. 应用场景

• 旋转矩阵

  • 旋转矩阵是与姿态一一对应，需要 9 个数来表示旋转，只有 3 个变量是独立的，常用于正逆解的运算；

• 旋转矢量

  • 旋转矢量的表示方法非常直观，只需要三个数就能表示旋转，常用于与用户的交互；
  • 旋转矩阵转换为旋转矢量时，数值对小角度的旋转敏感（除以$sin\theta$ ) ，且在 $R = I$ 时存在奇异；

• RPY 角

  • RPY 角采用三个角度表示姿态，常用于姿态的显示；

  • 存在万向锁问题，以及奇异问题（$\beta = \pm \pi/2$ 时）；

    如果 $\beta = \pi/2$ ，（$- \pi /2$ 同理）

    旋转矩阵为： $R = \left[ \begin{matrix} 0 & \sin(\gamma - \alpha) &cos(\gamma - \alpha)\\ 0 & \cos(\gamma - \alpha) & -sin(\gamma - \alpha)\\ -1 & 0 & 0\\ \end{matrix} \right]$

$\gamma$ 和 $\alpha$ 表示绕同一个轴旋转（-x），存在无数解（奇异），无论怎么改变  $\gamma$ 和 $\alpha$ 的值，只能实现绕 X 轴的旋转（万向锁）。

• 单位四元数

  • 采用单位四元数表示姿态可以避免数值奇异问题；
  • 常用于姿态的插值计算；

4. 参考

1. Modern_Robotics
2. 万向锁与欧拉角
3. 刚体姿态及旋转的表示方法